1. 🧭 왜 머신러닝에서 기초 수학이 중요한가?
머신러닝의 핵심 목표는 데이터에서 패턴을 찾아내는 것입니다.
이는 단순히 데이터를 넣고 결과를 보는 것이 아니라, 그 안에 숨겨진 구조를 수학적으로 모델링하는 일입니다. 예를 들어, 16세기 케플러는 브라헤가 수집한 천문 데이터를 분석하여 행성 운동 법칙을 도출했습니다. 이처럼 데이터에서 규칙을 찾아내는 일은 오랜 시간 인간이 해온 일이며, 머신러닝은 이를 수학적으로 자동화하는 기술입니다.
2. 📈 Polynomial Curve Fitting – 곡선을 이용한 함수 추정
이제 하나의 간단한 예제를 통해 머신러닝 모델의 기초를 살펴봅니다.
우리는 입력 와 출력 가 주어진 데이터셋이 있을 때, 이 관계를 다음과 같은 **다항식(polynomial)**으로 모델링할 수 있습니다.
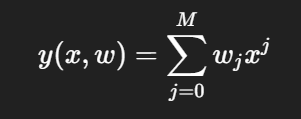
이 함수는 에 대해서는 비선형이지만, 모델 파라미터 에 대해서는 선형이라는 특징이 있습니다.
이제 이 모델이 실제 데이터를 잘 설명할 수 있도록 **오차 함수 **를 정의하고 이를 최소화하는 방향으로 파라미터 를 학습합니다.
하지만 여기서 문제가 생깁니다.
- M=0,1: 너무 단순해서 데이터를 잘 설명하지 못함 (언더피팅)
- M=9: 학습 데이터에는 딱 맞지만 너무 복잡해서 일반화가 안 됨 (오버피팅)
이를 해결하기 위해 사용하는 것이 **정규화(Regularization)**입니다.
정규화는 파라미터 w의 크기가 너무 커지는 것을 막는 방식으로 오버피팅을 방지하며, 머신러닝에서 매우 중요한 기법입니다. 이를 Ridge Regression 혹은 Neural Network에서는 Weight Decay라고도 부릅니다.
3. 🎲 Probability Theory – 확률 이론으로 불확실성을 다루다
현실 세계의 데이터는 항상 노이즈와 불확실성을 포함하고 있습니다.
그래서 머신러닝에서는 확률적 접근을 통해 이러한 불확실성을 정량적으로 다루는 것이 필요합니다.
가장 기초적인 두 가지 규칙은 다음과 같습니다:

이로부터 파생되는 베이즈 정리는 머신러닝에서 매우 핵심적인 역할을 합니다:

즉, 어떤 데이터 X를 관측한 후, 우리가 원하는 사건 Y가 얼마나 가능한지를 계산하는 방식입니다.
4. 📏 확률 분포와 기대값 – 평균, 분산, 공분산 이해하기
확률이론을 기반으로 우리는 기댓값(Expectation), 분산(Variance), 공분산(Covariance) 등을 계산할 수 있습니다.
이는 머신러닝 모델의 평균적인 행동이나 변수 간의 관계를 이해하는 데 매우 중요합니다.
- 기대값: 데이터의 평균적인 위치
- 분산: 얼마나 퍼져 있는가
- 공분산: 두 변수 사이의 관계 (같이 커지거나 같이 작아지는 경향)
5. 🎯 Bayesian Perspective – 확률을 믿음의 표현으로 해석하기
지금까지는 확률을 '빈도'로 해석하는 빈도주의(Frequentist) 관점이었습니다.
하지만 우리는 이제 베이즈주의(Bayesian) 관점으로 확장합니다.
베이즈 접근은 관측 데이터를 기반으로 **사전 신념(prior)**을 업데이트하여 **사후 확률(posterior)**을 계산합니다:
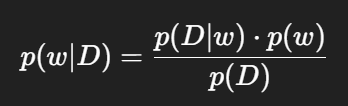
여기서 핵심은 우도(likelihood)와 사전 분포(prior)의 결합입니다.
이를 통해 우리는 단일 해를 찾는 것이 아니라, 모든 가능성을 확률적으로 고려할 수 있습니다.
6. 🧪 Gaussian Distribution – 가장 중요한 확률 분포
가장 널리 쓰이는 확률 분포는 바로 **정규분포(Gaussian distribution)**입니다.
1차원에서는 평균과 분산으로, 다차원에서는 평균 벡터와 공분산 행렬로 정의됩니다.
- 평균: 중심 위치
- 분산: 퍼짐 정도
- 공분산: 다차원 관계
이 분포는 모델링, 예측, 오류 분석 등에서 핵심적으로 사용됩니다.
7. 🧠 Curve Fitting – 확률 기반 함수 추정
이제 다시 curve fitting 문제로 돌아와, 확률적인 해석을 해봅니다.
출력 t가 입력 x에 대해 가우시안 분포로 분포한다고 가정하고, 이를 바탕으로 우도함수를 최대화하여 파라미터 를 추정합니다.

이를 통해 우리는 MLE (Maximum Likelihood Estimation) 또는 **MAP (Maximum A Posteriori)**로 파라미터를 추정할 수 있습니다.
8. 🤖 Bayesian Curve Fitting – 함수 자체도 확률적으로!
하지만 MAP도 결국 단일한 를 찾는 것이므로 완전한 베이즈 방식은 아닙니다.
완전 베이즈 추론에서는 의 모든 가능한 값에 대해 예측값의 확률 분포를 적분합니다:

이 결과는 다시 가우시안 분포로 표현되며, 예측값의 평균과 분산이 함께 제공됩니다.
9. 🧩 모델 선택과 차원의 저주
복잡한 모델이 항상 좋은 것이 아닙니다.
**모델 선택(model selection)**은 적절한 모델 복잡도를 결정하는 중요한 작업입니다. 이를 위해 보통 **교차검증(K-fold cross-validation)**을 사용합니다.
또한, 입력 차원이 증가하면 계산량과 필요 데이터 양이 급격히 늘어나는 차원의 저주(curse of dimensionality) 문제가 발생합니다. 이를 해결하기 위한 다양한 차원 축소 기법이나 정규화가 필요합니다.
10. 🧠 Decision Theory – 예측을 결정으로 바꾸는 방법
모델이 어떤 확률값을 출력했다면, 이제 우리는 이를 바탕으로 결정을 내려야 합니다.
이때 사용하는 것이 **의사결정 이론(Decision Theory)**입니다.
- 오분류 최소화: 가장 확률이 높은 클래스로 분류
- 기댓 손실 최소화: 잘못 분류될 경우의 비용까지 고려
- Reject Option: 확신이 낮을 때 판단을 유보하는 전략
11. 💡 Information Theory – 정보란 무엇인가?
마지막으로, 머신러닝의 핵심 개념 중 하나인 정보량과 엔트로피를 이해합니다.
- 정보량: 어떤 사건이 발생했을 때의 놀라움h(x)=−log2p(x

- 엔트로피: 평균 정보량 → 불확실성의 척도H(x)=−∑p(x)log2p(x)
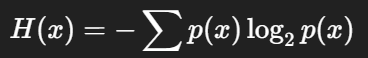
이 개념은 모델이 얼마나 예측하기 어렵고, 불확실성을 잘 설명하는지를 측정하는 데 활용됩니다.
✅ 마무리
이번 강의는 머신러닝을 공부함에 있어 반드시 필요한 수학적 토대를 다졌습니다.
각 주제는 서로 유기적으로 연결되어 있으며, 확률적 사고방식과 모델링의 구조적 이해를 중심으로 구성되어 있습니다.
다음 강의부터는 본격적으로 확률분포와 회귀 모델, 분류 모델로 들어갈 예정입니다.
'인공지능' 카테고리의 다른 글
| 시퀀스 데이터: RNN, LSTM, GRU 비교 (1) | 2025.05.08 |
|---|---|
| Advanced Machine Learning-04 : 선형 회귀 모델(Linear Regression Models) (0) | 2025.04.19 |
| Advanced Machine Learning-03: Probabilistic Distributions (0) | 2025.04.18 |
| 인공지능의 기초: AI의 개념과 작동 원리 이해하기 (0) | 2024.09.04 |